FlashAttention底层逻辑
提到大模型计算加速,FlashAttention 是绕不开的话题。它是一个在底层硬件上优化Attention 层计算的技术。网上介绍这个技术的博客很多,我本想转载一篇,但发现它们无非是把原论文翻译了一遍。它们会告诉你FlashAttention 调换了计算的顺序,从而减小了Q/K/V 矩阵被加载到片上SRAM 的次数,所以脱离了访存限制,加速了计算。但它们没有说为什么计算顺序可以交换,交换计算顺序后的结果为什么正确。如果仅仅是简单地把代码换一下行,那这个技术也没什么新鲜的。我把FlashAttention 读下来的感觉是它的底层逻辑其实非常巧妙,却几乎没有人注意到这一点。
本篇博客的目的是说清楚FlashAttention 的底层逻辑,当你理解它时,剩下的算法细节就一目了然了,甚至自己推导出FlashAttention 的算法流程也没有问题。我更希望今后大家遇到别的算子加速时,如果也能运用上FlashAttention 的核心思想,那是最好的。
在介绍FlashAttention 前,我必须首先介绍计算限制和访存限制(第一部分)和GPU 硬件结构(第二部分),来说明为什么减少访存次数可以减少计算时间。然后以Online Softmax 为例介绍FlashAttention 的核心思想(第三部分)。最后展示FlashAttention 的算法(第四部分),这时你会轻松读懂这个算法,也会理解为什么它能节省计算时间。
一、计算限制和访存限制
FlashAttention 一个很重要的改进点是:由于它发现Attention 层的计算瓶颈不在运算能力,而在读写速度上。因此它着手降低了对显存数据的访问次数,这才把整体计算效率提了上来。所以现在我们要问了:它是怎么知道卡点在读写速度上的?
为了解答这个问题,我们先来看几个重要概念:
- $\pi$: 硬件算力上限。指的是一个计算单元倾尽全力每秒钟所能完成的浮点运算数。单位是 FLOPS or FLOP/s 。
- $\beta$: 硬件带宽上限。指的是一个计算单元倾尽全力每秒所能完成的内存交换量。单位是Byte/s 。
- $\pi_t$ : 某个算法所需的总运算量,单位是FLOPs。下标$t$表示total。
- $\beta_t$: 某个算法所需的总数据读取存储量,单位是Byte。下标$t$表示total。
这里再强调一下对FLOPS和FLOPs的解释:
- FLOPS:等同于FLOP/s,表示Floating Point Operations Per Second,即每秒执行的浮点数操作次数,用于衡量硬件计算性能。
- FLOPs:表示Floating Point Operations,表示某个算法的总计算量(即总浮点运算次数),用于衡量一个算法的复杂度。
我们知道,在执行运算的过程中,时间不仅花在计算本身上,也花在数据读取存储上,所以现在我们定义:
- $T_{cal}$: 对某个算法而言,计算所耗费的时间,单位为秒,下标cal表示calculate。其满足$T_{cal}=\frac{\pi_t}{\pi}$。
- $T_{load}$: 对某个算法而言,读取存储数据所耗费的时间,单位为秒。其满足$T_{load}=\frac{\beta_t}{\beta}$。
我们知道,数据在读取的同时,可以计算; 在计算的同时也可以读取,所以我们有:
- T: 对某个算法而言,完成整个计算所耗费的总时间,单位为秒。其满足$T=\max(T_{cal}, T_{load})$。
也就是说,最终一个算法运行的总时间,取决于计算时间和数据读取时间中的最大值。
计算限制
当$T_{cal}>T_{load}$时, 算法运行的瓶颈在计算上,我们称这种情况为计算限制 (math-bound)。此时我们有: $\frac{\pi_t}{\pi}>\frac{\beta_t}{\beta}$,即:
\[\frac{\pi_t}{\beta_t}>\frac{\pi}{\beta}.\]内存限制
当$T_{cal}<T_{load}$时,算法运行的瓶到在数据读取上,我们称这种情况为内存限制 (memory-bound)。此时我们有$\frac{\pi_t}{\pi}<\frac{\beta_t}{\beta}$,即:
\[\frac{\pi_t}{\beta_t}<\frac{\pi}{\beta}.\]我们称$\frac{\pi_t}{\beta_t}$为算法的计算强度 (Operational Intensity)
Attention计算中的计算与内存限制
本节内容参考自:FlashAttention: 加速计算,节省显存, IO感知的精确注意力
有了上述前置知识, 现在我们可以来分析影响Transformer 计算效率的因素到底是什么了。我们把目光聚焦到attention 矩阵的计算上,假设序列输入长度是$N$,其计算复杂度为$O(N^2)$,是Transformer 计算耗时的大头。
假设我们现在采用的硬件为A100-40GB SXM,同时采用漉合精度训练 (可理解为训练过程中的计算和存储都是fp16形式的,一个元素占用2byte)
\[\frac{\pi}{\beta}=\frac{312*10^{12}}{1555*10^9}=201\text{FLOPs/Bytes}\]假定我们现在有矩阵$Q,K\in\mathbb{R}^{N*d}$,其中$N$为序列长度,$d$为embedding dim 。现在我们要计算$S=QK^T$,则有:
\[\frac{\pi_t}{\beta_t}=\frac{2N^2d}{2Nd+2Nd+2N^2}=\frac{Nd}{2d+N}.\]从这个公式可以看出,当$N$和$d$越大时,计算强度越大,越容易受到计算限制。不同$N,d$取值下的受限类型如下:
| $N$ | $d$ | ops/bytes | 受限类型 |
|---|---|---|---|
| 256 | 64 | 43 | <201, meomery-bound |
| 2048 | 64 | 60 | <201, meomery-bound |
| 4096 | 64 | 62 | <201, meomery-bound |
| 256 | 128 | 64 | <201, meomery-bound |
| 2048 | 128 | 114 | <201, meomery-bound |
| 4096 | 128 | 120 | <201, meomery-bound |
| 256 | 256 | 85 | <201, meomery-bound |
| 2048 | 256 | 205 | >201, calculation-bound |
| 4096 | 256 | 228 | >201, calculation-bound |
根据这个表格,我们可以来做下总结:
- 计算限制(calculation-bound):大矩阵乘法($N$和$d$都非常大)、通道数很大的卷积运算。相对而言,读得快,算得慢。
- 内存限制(memory-bound):逐点运算操作。例如:激活函数、dropout、mask、softmax、BN和LN。相对而言,算得快,读得慢。
所以,“Transformer计算受限于数据读取”也不是绝对的,要综合硬件本身和模型大小来综合判断。但从表中的结果我们可知,memory-bound的情况还是普遍存在的,所以Flash attention的改进思想在很多场景下依然适用。
在Flash attention中,计算注意力矩阵时的softmax计算就受到了内存限制,这也是flash attention的重点优化对象,我们会在下文来详细看这一点。
roof-line模型
一个算法运行的效率是离不开硬件本身的。我们往往想知道: 对于一个运算量为$\pi_t$,数据读取存储量为$\beta_t$的算法, 它在算力上限为$\pi$,带宽上限为$\beta$,的硬件上, 能达到的最大性能$P$(Attanable Performance)是多少?
这里最大性能$P$指的是当前算法实际运行在硬件上时,每秒最多能达到的计算次数, 单位是FLOP/S。
Roof-line模型就是为了解答这一问题而提出的,它能直观帮我们看到算法在硬件上能跑得多快,模型见下图。
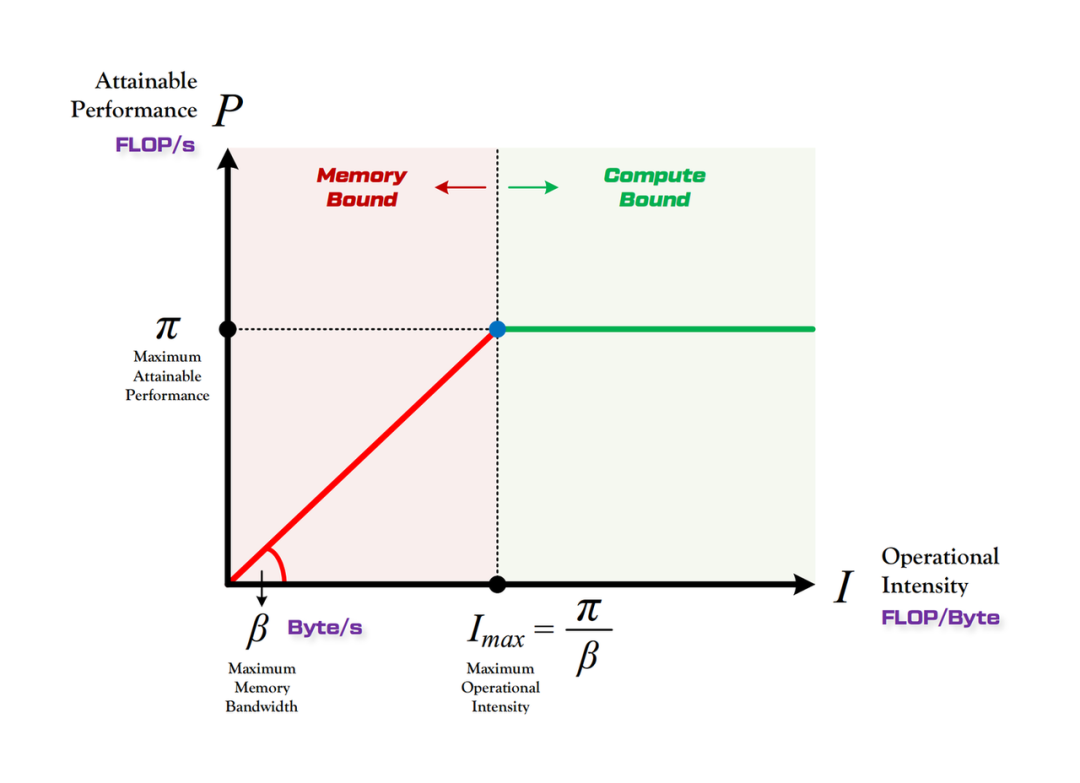
如图, 横坐标$I$表示计算强度, 满足$I=\frac{\pi_t}{\beta_t}$;纵坐标$P$表示算法运行在硬件上的性能。算法的运行性能不会超过硬件本身的计算上限,所以$P$的最大值取到$\pi$。根据我们之前的分析,当$I>\frac{\pi}{\beta}$时,存在计算限制;当$I<\frac{\pi}{\beta}$时,存在内存限制。
二、GPU上的存储与计算
由于Flash attention的优化核心是减少数据读取的时间,而数据读取这块又离不开数据在硬件上的流转过程,所以这里我们简单介绍一些GPU上的存储与计算内容,作为Flash attention的背景知识。
GPU的存储分类
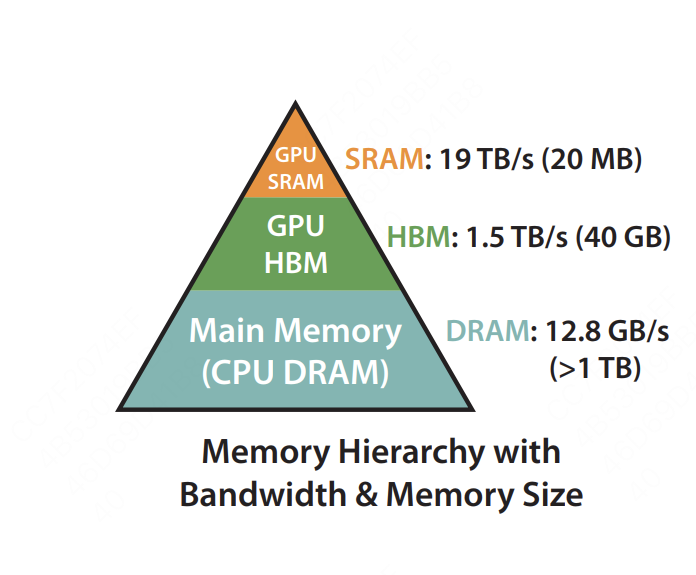
上图是FlashAttention论文所绘制的硬件不同的存储类型、存储大小和带宽。一般来说,GPU上的存储分类,可以按照是否在芯片上分为片上内存(on chip)和片下内存(off chip) 。
- 片上内存:主要用于缓存(cache)及少量特殊存储单元(例如texture),其特点是 “存储空间小,但带宽大”。对应到上图中,SRAM就属于片上内存,它的存储空间只有20MB,但是带宽可以达到19TB/s。
- 片下内存:主要用于全局存储(global memory),即我们常说的显存,其特点是 “存储空间大,但带宽小”,对应到上图中,HBM就属于片下内存(也就是显存),它的存储空间有40GB(A100 40GB),但带宽相比于SRAM就小得多,只有1.5TB/s。
当硬件开始计算时,会先从显存(HBM)中把数据加载到片上(SRAM),在片上进行计算,然后将计算结果再写回显存中。那么这个“片上”具体长什么样,它又是怎么计算数据的呢?
GPU是如何做计算的
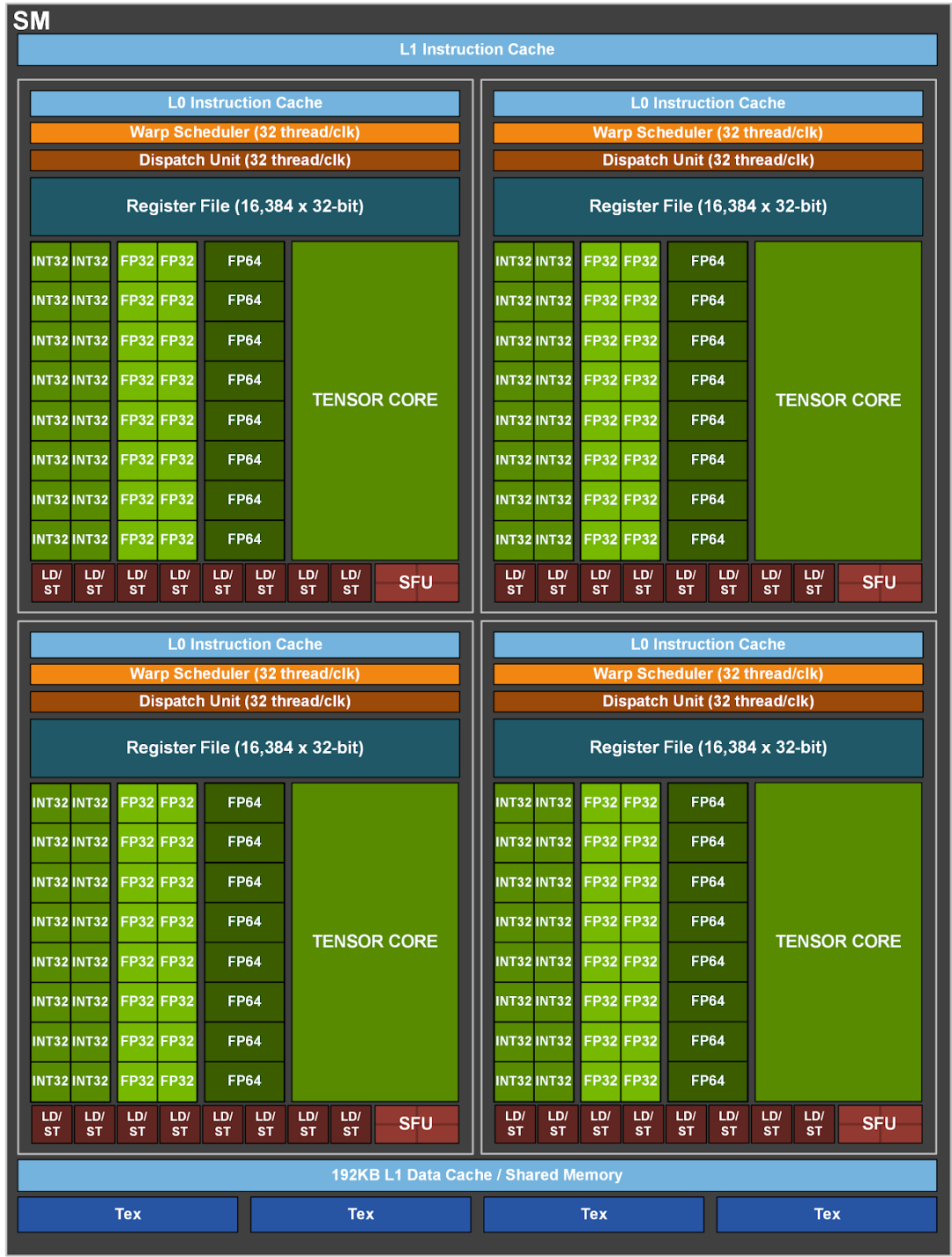
如图,负责GPU计算的一个核心组件叫SM(Streaming Multiprocessors,流式多处理器),可以将其理解成GPU的计算单元,一个SM又可以由若干个SMP(SM Partition)组成,例如图中就由4个SMP组成。SM就好比CPU中的一个核,但不同的是一个CPU核一般运行一个线程,但是一个SM却可以运行多个轻量级线程(由Warp Scheduler控制,一个Warp Scheduler会抓一束线程(32个)放入cuda core(图中绿色小块)中进行计算)。
我们将上图所示的结构再做一次简化:
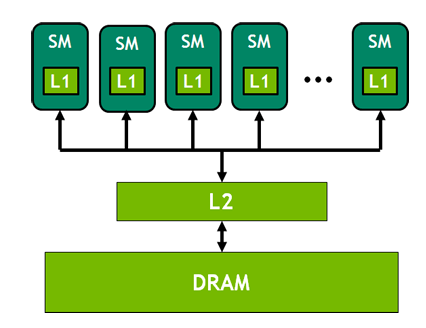
- DRAM:可以理解成是全局存储,也即可以当成是我们的显存
- L1缓存:每个SM都有自己的L1缓存,用于存储SM内的数据,被SM内所有的cuda cores共享。SM间不能互相访问彼此的L1。FlashAttention 中SRAM是on-chip的,对应到这里就是L1缓存。
- L2缓存:所有SM共享L2缓存。L1/L2缓存的带宽都要比显存的带宽要大,也就是读写速度更快,但是它们的存储量更小。
现在我们再理一遍GPU的计算流程:将数据从显存(HBM)加载至on-chip的SRAM中,然后由SM读取并进行计算。计算结果再通过SRAM返回给显存。
我们知道显存的带宽相比SRAM要小得多,读一次数据是很费时的,但是SRAM存储又太小,装不下太多数据。所以我们就以SRAM的存储为上限,尽量保证每次加载数据都把SRAM给打满,节省数据读取时间。
kernel融合
前面说过,由于从显存读一次数据是耗时的,因此在SRAM存储容许的情况下,能合并的计算我们尽量合并在一起,避免重复从显存读取数据。
举例来说,我现在要做计算A和计算B。在老方法里,我做完A后得到一个中间结果,写回显存,然后再从显存中把这个结果加载到SRAM,做计算B。但是现在我发现SRAM完全有能力存下我的中间结果,那我就可以把A和B放在一起做了,这样就能节省很多读取时间,我们管这样的操作叫kernel融合。
由于篇幅限制,我们无法详细解释kernel这个概念,在这里大家可以粗犷地理解成是“函数”,它包含对线程结构(grid-block-thread)的定义,以及结构中具体计算逻辑的定义。理解到这一层已不妨碍我们对FlashAttention 的解读了,想要更近一步了解的朋友,推荐阅读这篇(CUDA编程入门极简教程)文章。
kernel融合和尽可能利用起SRAM,以减少数据读取时间,都是flash attention的重要优化点。在后文对伪代码的解读中我们会看到,分块之后FlashAttention将矩阵乘法、mask、softmax、dropout操作合并成一个kernel,做到了只读一次和只写回一次,节省了数据读取时间。
好!目前为止所有的背景知识我们都介绍完了,现在我们直入主题,看看FlashAttention 到底是怎么巧妙解决memory-bound 问题。
三、从Safe softmax 到 Online softmax
在计算Attention 的过程中,有一个softmax 的操作。这步操作的含义是将token 之间的Attention 分数映射到$(0,1)$区间内。公式为:
\[\text{softmax}(\{x_1,x_2,\cdots,x_N\})=\left\{\frac{e^{x_1}}{\sum_{j=1}^Ne^{x_j}},\frac{e^{x_2}}{\sum_{j=1}^Ne^{x_j}},\cdots,\frac{e^{x_N}}{\sum_{j=1}^Ne^{x_j}}\right\}.\]而如果$x_i$过大, 那么在计算softmax 的过程中, 就可能出现数据上溢的情况。为了解决这个问题, 我们可以采用Safe softmax 方法:
\[m(\mathbf{x})=\max_ix_i,\] \[\text{softmax}(\mathbf{x})=\left\{\frac{e^{x_1-m(\mathbf{x})}}{\sum_{j=1}^Ne^{x_j-m(\mathbf{x})}},\frac{e^{x_2-m(\mathbf{x})}}{\sum_{j=1}^Ne^{x_j-m(\mathbf{x})}},\cdots,\frac{e^{x_N-m(\mathbf{x})}}{\sum_{j=1}^Ne^{x_j-m(\mathbf{x})}}\right\}.\]这样$x_j-m(\mathbf{x})$是一个非正数,$0<e^{x_j-m(\mathbf{x})}\leq1$,就不会溢出了。于是我们可以想到一个简单的计算Safe softmax 的算法如下:

它需要三次循环来计算,意味着至少需要$3N$次读数据和写数据操作。我们上面提到过,读写太频繁会使得GPU受到内存限制,我们应该通过改变计算顺序来减少读写显存(片下内存)的次数。缩减循环的个数可以减少读写的次数。观察这个算法,你会发现它三个循环不能被合并的原因是
- 每个$d_i$的计算依赖于$m_N$,所以不能和第一个循环合并;
- 每个$a_i$的计算依赖于$d_N$,所以不能把后两个循环合并。
如何打破$d_i$对$m_N$的依赖、$a_i$对$d_N$的依赖,从而合并循环呢?这是一个问题,同时也是FlashAttention 最巧妙的地方。
首先,
\[d_i=\sum_{j=1}^ie^{x_j-m_N},\]但其实我们并不需要知道每一个$d_i$等于多少,我们只要拿到最后的$d_N$就可以了。所以思路就是我可以构造一个数列${d_i’}$,使得
- $d_i’$的计算不需要知道$m_N$,只需要知道$d_1’,d_2’,\cdots,d_{i-1}’$和$m_1,m_2,\cdots,m_i$;
- $d_N’=d_N$是我们需要的结果。
想到了这个思路,我们就把$d_i$公式里$m_N$的下标修改一下,就变成了
\[d_i'=\sum_{j=1}^ie^{x_j-m_i},\]它显然满足上述的两个要求,因为$i=N$时,$d_i’=d_i$。并且
\[\begin{aligned} d_i'=&\sum_{j=1}^ie^{x_j-m_i}\\ =&\sum_{j=1}^{i-1}e^{x_j-m_i}+e^{x_i-m_i}\\ =&\sum_{j=1}^{i-1}e^{x_j-m_{i-1}}\cdot e^{m_{i-1}-m_i}+e^{x_i-m_i}\\ =&d_{i-1}'\cdot e^{m_{i-1}-m_i}+e^{x_i-m_i}. \end{aligned}\]递推公式也有了,好,我们把算法整理一下,这就是Online softmax 算法:

以上优化对于 softmax 操作来说已经到头了,我们不可能在一次循环中把 softmax 的结果计算出来。因为向量中的每个元素都是独立的,不可能在没有遍历到后续元素的情况下,确定当前元素最终的 softmax 值。
四、FlashAttention
FlashAttention其实也是上述的思想,现在我们趁热打铁,推导FlashAttention 的算法流程。引入Online softmax 后,计算Attention 的算法如下:

我们重复上文的思路:我们并不需要知道每一个$\mathbf{o}_i,a_i$等于多少,我们只要拿到最后的$\mathbf{o}_N$就可以了。我可以构造一个数列${\mathbf{o}_i’}$,使得
- $\mathbf{o}_i’$的计算不需要知道 $d_N’,m_N$,只需要知道 $d_1’,d_2’,\cdots,d_i’$和$m_1,m_2,\cdots,m_i$;
- $d_N’=d_N$是我们需要的结果。
那么用同样的技巧修改$\mathbf{o}_i$为$\mathbf{o}_i’$:
\[\mathbf{o}_i'=\sum_{j=1}^i\frac{e^{x_j-m_i}}{d_i'}V[j:]\]并且
\[\begin{aligned} \mathbf{o}_i'=&\sum_{j=1}^i\frac{e^{x_j-m_i}}{d_i'}V[j:]\\ =&\sum_{j=1}^{i-1}\frac{e^{x_j-m_i}}{d_i'}V[j:]+\frac{e^{x_i-m_i}}{d_i'}V[i:]\\ =&\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}'}V[j:]\cdot\frac{d_{i-1}'}{d_i'}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i'}V[i:]\\ =&\mathbf{o}_{i-1}'\cdot\frac{d_{i-1}'e^{m_{i-1}-m_i}}{d_i'}+\frac{e^{x_i-m_i}}{d_i'}V[i:]. \end{aligned}\]经过这次优化,整个算法被优化成了一次循环,这就是FlashAttention 的原型:

最后的一点细节就是使用了Tiling 技术。Tile 的意思是分块,Tiling 无非就是分块矩阵乘法。使用分块矩阵是因为片上内存非常小,只能一部分一部分地把矩阵的每个分块加载进来进行计算。以对矩阵$K$进行分块为例,假如把$K$分为$b$块,算法应改成下面的图片,区别是一次循环$N$轮变为了循环$\frac{N}{b}$轮,进一步减少了读写次数。

最后我们再回来看FlashAttention 原论文的算法,想必你已经没有什么疑问了。

五、FlashAttention V2的小改进
FlashAttention 的第二个版本就都是小改进了,它的创新性就没有第一个版本那么大了。
调整内外循环
FlashAttention V1 中采用了一个非直觉的外层循环矩阵$K,V$,内层循环矩阵$Q,O$的方式,这会导致矩阵$O$被额外加载。事实上,在FlashAttention V2 出来之前,很多FlashAttention 的实现就修改了这个循环顺序。
减少了非矩阵乘法的运算次数
现代GPU对矩阵乘法有专门的硬件优化,矩阵乘法FLOPS是非矩阵乘法FLOPS的16倍左右。具体实现上,FlashAttention V1 每轮迭代都有一个rescale 操作:

在V2 中,不再在每轮迭代中都除以$d_i’$,而是等循环体结束以后,对计算得到的$\mathbf{o}_N’$统一除以$d_N’$。
Warp Level 并行度
假设一个 block 实际上会被 SM 划分成 4 个 warp,在 V1 版本中,矩阵$K,V$的 block 会被划分成 4 个 warp,每个 warp 计算$Q_iK_j^\top$后会得到一个$B_r\times\frac{B_c}{4}$的矩阵,需要 4 个 warp 全部计算完以后,把四个矩阵排成一行(下图中 V1 版本红色的四个矩阵),才能计算softmax$(Q_iK_j^\top)$真正的值,这个过程中存在 warp 之间的通信。
